694. Семье, состоящей из бабушки, папы, мамы, дочери и сына подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи?

  Решение:

  У первого члена семьи (например, бабушки) есть 5 вариантов выбора, у следующего (пусть это будет папа) остаётся 4 варианта выбора, следующий (например, мама) будет выбирать уже из 3 чашек, следующий - из двух, последний же получает одну оставшуюся чашку. Покажем эти способы на схеме.

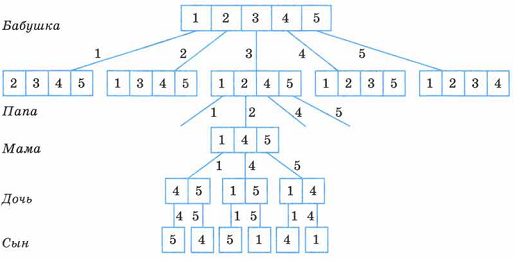
  Получили, что каждому выбору чашки бабушкой соответствует четыре возможных выбора папы, т.е. всего 5 · 4 способов. После того как папа выбрал чашку, у мамы есть три варианта выбора, у дочери - два, у сына - один, т.е. всего 3 · 2 · 1 способов. Окончательно получаем, что для решения задачи надо найти произведение 5 · 4 · 3 · 2 · 1.

  Заметим, что получили произведение всех натуральных чисел от 1 до 5. Такие произведения записывают короче:

5 · 4 · 3 · 2 · 1 = 5! (читают "пять факториáл")

 Итак, ответ задачи: 5! = 120, т.е. чашки между членами семьи можно распределить ста двадцатью способами.